Rhombitriheptagonal tiling

Rhombitriheptagonal tiling

Poincaré_disk_model
Type Hyperbolic semiregular tiling
Vertex figure 3.4.7.4
Schläfli symbol 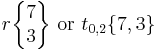r\begin{Bmatrix} 7 \\ 3 \end{Bmatrix}\text{ or }t_{0,2}\{7,3\}
Wythoff symbol 3 | 7 2
Coxeter-Dynkin
Symmetry [7,3]
Dual Deltoidal triheptagonal tiling
Properties Vertex-transitive

In geometry, the rhombitriheptagonal tiling is a semiregular tiling of the hyperbolic plane. At each vertex of the tiling there is one triangle and one heptagon, alternating between two squares. The tiling has Schläfli symbol t0,2{7, 3}.

Contents

Related polyhedra and tilings

This tiling is topologically related as a part of sequence of cantellated polyhedra with vertex figure (3.4.n.4), and continues as tilings of the hyperbolic plane. These vertex-transitive figures have (*n32) reflectional symmetry.


(3.4.3.4)
(*332)
(3.4.4.4)
(*432)
(3.4.5.4)
(*532)

(3.4.6.4)
(*632)
(3.4.7.4)
(*732)
(3.4.8.4)
(*832)

Dual tiling

The dual tiling is called a deltoidal triheptagonal tiling, and consists of congruent kites. It is formed by overlaying an order-3 heptagonal tiling and an order-7 triangular tiling.

See also

References

External links